6º EN MATILLAS: FRACCIONES

Otras viejas conocidas. Vamos, que no tienes excusa para bordar este tema.

Ya sabemos que podemos expresar las cantidades de formas muy variadas. Las fracciones son una de esas formas.

Te voy a contar una historia:

El día del cumple de la hermana de Juan su mamá había preparado una deliciosa tarta de chocolate, precisamente la preferida de Juan.
Cuando llegó la hora de la fiesta, mamá salió de la cocina enfadadísima, fue directa a Juan y le riñó mucho, muchísimo.
Juan se disculpaba diciendo que él sólo había comido una fracción de la tarta, para ser exactos 8/8, no era para tanto... ¿o sí...?

¿Crees que el enfado de la mamá de Pablo está justificado?

CONCEPTO DE FRACCIÓN

Una fracción expresa un cociente, una división entre dos números. El de abajo, que se llama denominador, me dice en cuántas partes está dividida la unidad. El de arriba, el numerador, lo que me cuenta es cuántas partes estoy cogiendo. Por lo tanto, cuando el numerador y el denominador son iguales lo que significa es que cojo todas las partes en que está dividida la unidad, es decir, lo cojo todo.

De esta forma, una fracción puede representar cantidades iguales a la unidad, cuando numerador y denominador son iguales, cantidades menores que la unidad, cuando el numerador es más pequeño que el denominador, y cantidades mayores que la unidad, cuando el numerador es mayor que el denominador, eso significa que me he comido una parte entera y una fracción de otra.

Vamos a ponerlo en práctica, puedes ejercitarte a continuación:

COMPARAR FRACCIONES

Podemos jugar con las fracciones, las podemos transformar en un número decimal: Para pasar una fracción a un número decimal se divide el numerador entre el denominador.
• Hay divisiones cuyo resultado en un número natural.
• Otras divisiones su resultado es un número decimal con algunas cifras decimales.
• Otras divisiones su resultado es un decimal periódico, que tiene un grupo de cifras decimales que se repiten y por muchas cifras decimales que saquemos no se llega a tener de resto 0.

Y también podemos pasar un decimal a fracción : Para escribir un número decimal no periódico en forma de fracción se pone de numerador el número sin la coma y de denominador el 1 seguido de tantos 0 como cifras decimales tenga el número decimal.

Y otra cosa: Un número natural es una fracción que tiene como numerador el número natural y como denominador el 1.

¡ QUÉ FÁCIL! YA OS LO DIJE

NÚMEROS MIXTOS

Mira estas fracciones: 13/4; 17/5; 9/2

Si te das cuenta, aunque el numerador es mayor que el denominador, no equivalen a un número natural; es decir, la división entre el numerador y el denominador no es exacta. Sin embargo, también las puedo expresar de otra manera: son los NÚMEROS MIXTOS, formados por un número natural seguido de una fracción.

¿Qué significa que he comprado 13/4 de empanada?

1.- Que las empanadas están divididas en 4 porciones.

2.- Que he comprado 13 porciones.

3.- Por tanto eso equivale a 3 empanadas enteras -12/4- más 1/4 de otra empanada.

4.- Eso se representa con un número mixto:3 ¼

Puedes mirar aquí para saber más sobre los números mixtos:

NÚMEROS MIXTOS EXPLICACIÓN

FRACCIÓN DE UN NÚMERO

Como ya hemos dicho una fracción expresa una cantidad determinada, no es más que una división. En ocasiones las fracciones vienen relacionadas con un número, es decir, lo que tengo que averiguar es la fracción de un determinado número. Por ejemplo, si he realizado los 3/5 de los 20 ejercicios de matemáticas, eso quiere decir que he hecho 12 ejercicios. Te adjunto un enlace donde lo explica muy bien, espero que lo comprendas.

FRACCIÓN DE UN NÚMERO

$fracción de un número$

FRACCIONES EQUIVALENTES

Vamos a probar tus dotes deductivas. ¿qué significa eso de equivalentes?, ya sabes que el prefijo "equi-" significa igual, y ¿qué puede significar "-valente"? Eso es, equivalentes significa de igual valor, es decir, son formas distintas de expresar una misma cantidad.

1	=	2	=	4

2		4		8

Y en un dibujo se ve así:

1/2		2/4		4/8
	=		=

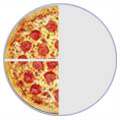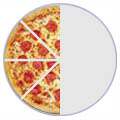Si te fijas, lo que estamos haciendo es multiplicar el numerador y el denominador pro el mismo número, de este modo la fracción mantiene su valor, es decir, sigue representando la misma cantidad de pizza. La regla a recordar es:

¡Lo que haces a la parte de arriba de la fracción también lo tienes que hacer a la parte de abajo!

Por eso, estas fracciones son en realidad la misma:

	× 2		× 2

1	=	2	=	4

2		4		8

	× 2		× 2

También puedo lograr fracciones equivalentes dividiendo, en vez de multiplicando, el numerador y el denominador por el mismo número.

	÷ 3		÷ 6

18	=	6	=	1

36		12		2

	÷ 3		÷ 6

Lo único que debes de tener en cuenta es que cuando lo que hago es dividir tengo que buscar un número que sea divisor a la vez del número que está en el numerador y del número que está en el denominador, la división tiene que se exacta, por lo tanto tengo que buscar divisores comunes. Recuerda el tema de la divisibilidad.

Cuando busco fracciones equivalentes a una dada por este método de dividir los dos términos de la fracción lo que consigo son fracciones cada vez más pequeñas, las estoy reduciendo o simplificando, hasta llegar a un punto en que ya no puede ser más pequeña, esa fracción se llama IRREDUCIBLE.

Para ver más cosas:

FRACCIONES EQUIVALENTES
LIBROS VIVIOS SM
ANAYA

Las fracciones equivalentes nos pueden resultar muy útiles.
Cuando comparamos fracciones la tarea puede ser muy sencilla: si tenemos el mismo denominador la fracción más grande es la que tiene el numerador mayor, en el caso de que tengan el mismo numerador la fracción más grande es la que tiene el denominador más pequeño (los trozos son más grandes, luego representa mayor cantidad).
COMPARAR FRACCIONES

Pero también puede ser muy complicada, cuando tenemos que comparar fracciones de distintos denominadores y distintos numeradores. ¿Qué hacemos entonces?
Aquí es donde intervienen las fracciones equivalentes.
Se trata de cambiar las fracciones que me dan por otras que valgan lo mismo pero con las que me resulte más fácil trabajar, es decir, voy a buscar fracciones equivalentes a las que me dan con un denominador igual, esto es lo que se llama COMÚN DENOMINADOR
Aquí tienes un enlace que te enseña a reducir a común denominador.

Y para terminar, como siempre, el cuadernillo de clase para poder seguir trabajando:

OPERACIONES CON FRACCIONES

Ahora que ya hemos repasado un montón de cosas de "nuestras amigas las fracciones" es el momento de dar un paso más.
Casi sin querer, cuando hemos jugado con la idea de la fracción como una parte de la unidad, hemos calculado cuánto falta para llegar a la unidad completa, o qué parte de esa unidad hemos reunido entre varios... Es decir, así, despacito, sin darnos cuenta hemos sumado y restado fracciones.
No ha sido difícil, nos ha salido de forma natural. Bueno, pues ha llegado el momento de que sigamos aprendiendo.

MUY FÁCIL PARA SUMAR Y RESTAR FRACCIONES

SUMAS Y RESTAS DE FRACCIONES CON EL MISMO DENOMINADOR

SUMAS DE FRACCIONES CON DISTINTO DENOMINADOR

RESTAS DE FRACCIONES DE DISTINTO DENOMINADOR

ANAYA OPERACIONES CON FRACCIONES

¡¡¡No es un trabalenguas!!!

¿Cuánto son los 2/3 de los 3/4 de una tableta de chocolate?

Vamos a ver si lo entiendo. Primero divido la tableta en 4 trozos y cojo 3 y de esos tres cojo 2/3, o sea, los divido en tres y cojo dos, ¿no es eso?

►3/4

Es como si lo dividimos en 12 cachos y cogemos 6

►2/3

El resultado de multiplicar fracciones es una fracción, cuyo numerador es el producto de los numeradores y el denominador el producto de los denominadores. ¡QUÉ FÁCIL!

Fíjate: los 2/3 de los 3/4 son 6/12. Lo que hemos hecho ha sido multiplicar.

MULTIPLICACIÓN DE FRACCIONES

Para dividir fracciones multiplicamos los términos en cruz. Es decir, el numerador de la primera por el denominador de la segunda, este será el numerador; y el denominador de la primera por el numerador de la segunda, ese será el denominador.
NO OLVIDES QUE UN NÚMERO ENTERO ES UNA FRACCIÓN CUYO NUMERADOR ES EL NÚMERO Y EL DENOMINADOR 1.

¿Cuántas botellas de 3/4 de litro se pueden llenar con una garrafa de 30 litros? Claro, lo que tengo que hacer es dividir: